昨日に引き続き、ホワイトボード演習の体験授業です。
今日は私立中学中2生。私立なので学習進度はかなり早いです。今日のテーマは図形(中点連結定理)。
本日あつかった問題を紹介します。是非皆さんもチャレンジしてみてください。
問題
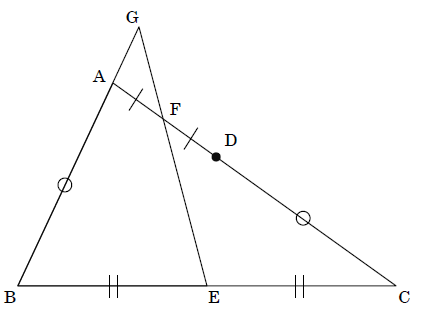
AB < AC である △ABC において, 次のような点をとる。
・D は AC 上の点で, CD = AB
・BC の中点 E , AD の中点 F
・直線 AB と直線 EF の交点 G
このとき, AF = AG であることを証明せよ。
【解説】
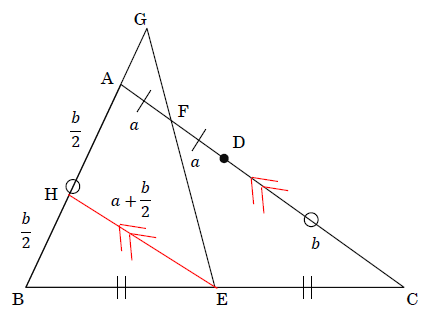
補助線を引いて考えます。
上の図のように, 点 E を通り線分 AC に平行な直線を引き, 線分 AB との交点を点 H とします。
仮定より
AF = FD = \(a\)
CD = AB = \(b\)
△ABC において, 中点連結定理の逆より
AH = BH = \(\frac{b}{2}\)
EH = \(a+\frac{b}{2}\)
AG = \(x\) とおくと
△GAF ∽ △GHE より
\(x : \left( x+\frac{b}{2} \right) = a : \left( a+\frac{b}{2} \right) \)
\(x=a\)
よって
AF = \(a\), AG = \(a\)
ゆえに, AF = AG ・・・(終)




