中１数学の授業開始小テストで取り上げた過去問。
令和５年度巣鴨高校の数学入試問題です。テーマは関数と図形。
(1)(2)基本、(3)標準、(4)応用でしょうか。
(4)が合否を分ける問題かも。
良問なので、是非取り組んでみてください。
下図のように、 \(x\) 座標が \(-2\) の点 A で、放物線 \(y=x^2\) と双曲線 \(y=\dfrac{a}{x}\) （\(a<0\)）が交わっています。放物線 \(y=x^2\) 上に点 B\((1, 1)\) をとり、直線 AB と双曲線 \(y=\dfrac{a}{x}\) の点 A と異なる交点 C 、直線 AB と \(y\) 軸との交点を D とします。
このとき、次の各問いに答えなさい。
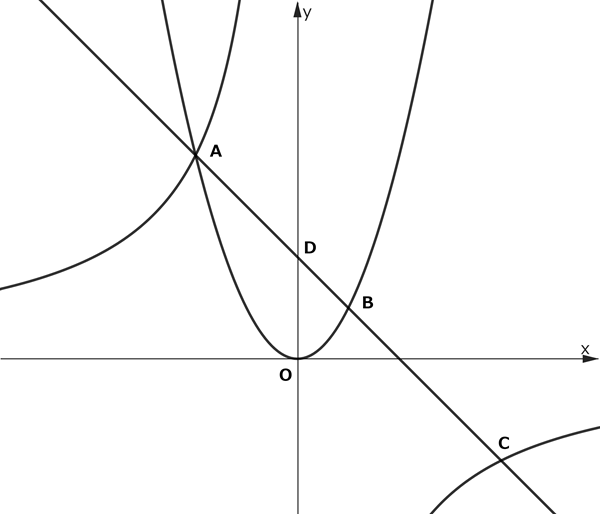
(2) 直線 AB の式を求めなさい。
以下、原点に関して点 A と対称な点を E とします。
(3) △ACE の面積を求めなさい。
(4)
点 P は放物線 \(y=x^2\) 上を点 A から点 B まで動きます。直線 DP が △ACE を２つの部分に分け、その２つの部分の面積比が２：１になるときの点 P の \(x\) 座標をすべて求めなさい。
引用：巣鴨高校
