本日の指導は扇形の面積公式の導出と利用についてです。
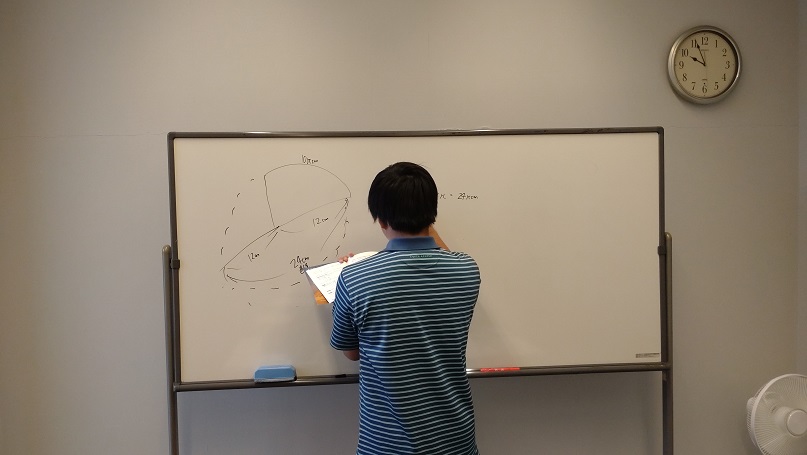
半径が \(R\)、弧の長さが \(l\) の扇形の面積 \(S\) は
\(S=\dfrac{1}{2}lR\)
と表されます。
これは円周 \(2\pi R\) に対する弧の長さ \(l\) の割合から求めることができます。
円の面積は \(\pi R^2\) なので
\(S=\pi R^2 \times \dfrac{l}{2\pi R}\)
\(=\dfrac{1}{2}lR\)
となります。公式は導出してから利用すると理解も深まります。
また、公式の使う練習後に改めて導出を考察するもの良い勉強になります。
今日は、数検3級合格の報告を頂きました!
中学に入学して半年が経ちませんが、中学数学の基本はマスターしたといって良いかと思います。
今後は高校数学に進んでいきます!
数学の先取り学習をしたい方は是非お問い合わせください。