茨城県立高校入試を受験した皆さんお疲れ様でした。
数学の最後の問題、大問６は例年立体の問題が出題されますが、今年も立体が出題されました。
ということで、大問６（２）② の問題を紹介します。来年受験生また、県外の方も是非チャレンジしてみてください。
※ 表現を若干変更してあります。
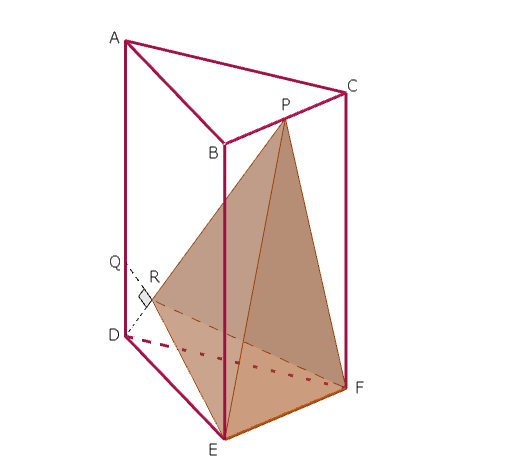
図のように、DE=DF= 3 cm、EF= 2 cm の三角形を底面とし、高さが 4 cm の三角柱 ABCDEFがある。
辺BCの中点を P とし、辺 AD 上に AQ：QD = 3：1 となる点 Q をとる。また、線分 DP 上に∠QRD= 90°となる点 R をとる。
このとき、三角すい RPEF の体積を求めなさい。
【解答例】
△DRQ ∽ △DAP （相似条件：２組の角がそれぞれ等しい）
相似比 \(1：2\sqrt{6}\) より
DR \(=\dfrac{\sqrt{6}}{3}\)
したがって
DP：DR \(=6：1\)
つまり DP：RP \(=6：5\)
したがって、三角すい RPEF の高さは
\(2\sqrt{2}\times \dfrac{5}{6}\)
\(=\dfrac{5\sqrt{2}}{3}\)・・・①
底面積は
\(2\times 4 \times \dfrac{1}{2}\)
\(=4\)・・・②
①, ②より三角すい RPEF の体積は
\(4\times \dfrac{5\sqrt{2}}{3}\times \dfrac{1}{3}\)
\(=\dfrac{20\sqrt{20}}{9}\) ㎠・・・（答）
