昨日の【解いてみよう!】の解答編です。
まずは、問題を再掲。
【問題】
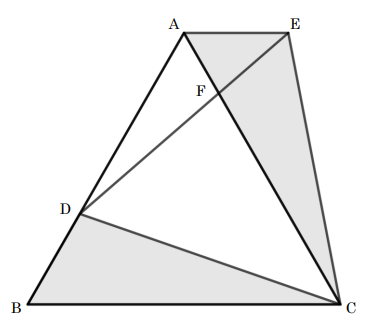
図のように、1辺の長さ6の正三角形ABCにおいて、BD=2となるように点Dをとります。△DBCを点Cを中心として、点Bが点Aに重なるように回転移動し△EACとします。線分ACとDEの交点をFとするとき、線分CFの長さを求めなさい。
【解答】
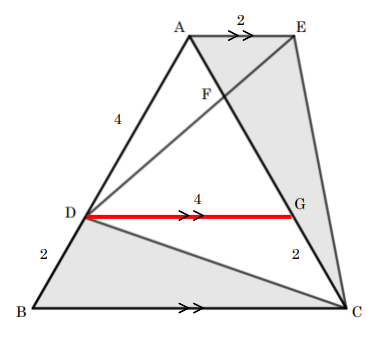
図のように、線分BCに平行な直線を引き(補助線)、線分ACとの交点をGとします。
BC//AE(∵錯角60°)より、DG//AE。
2つの角がそれぞれ等しいので△FAE∽△FGDとなり、相似比は2:4=1:2となります。
AG\(=4\) より、FG\(=\dfrac{2}{3}\times 4=\dfrac{8}{3}\)
また、CG\(=2\) より

補助線DGを引くのがポイントだね!





