
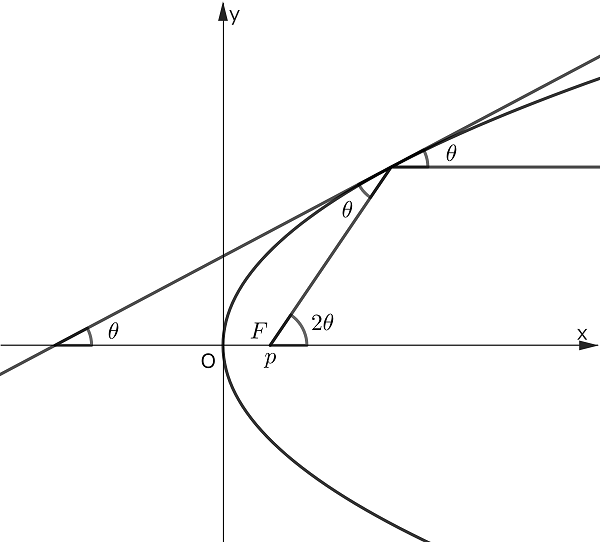
放物線をその軸のまわりに回転させて得られる形の凹面鏡を作ると、軸に平行に入ってきた光は、この鏡面で反射し、放物線の焦点Fを必ず通過します。衛星から電波を受信するときに利用されるパラボロアンテナにも、この原理が利用されています。
放物線の式は
と表され、焦点の座標は
したがって、図より反射後の直線の傾きは
と表され、焦点の座標は
したがって、図より反射後の直線の傾きは
研究学園都市つくばより配信中!算数・数学、理科専門オンライン個別指導塾。小学生・中学生の高校数学理科「先取り学習+数検・理検合格」で生涯役立つ自立的な学びを推進しています。全国47都道府県対応。