毎月、埼玉県岩槻の情報誌「ら・みやび」の脳トレ問題に挑戦しています。
この脳トレの面白いところは、問題文は平易なので小学生から大人まで取り組むことができますが、簡単には答えが導かれないところにあります。頭を柔らかくして考えるのが大切です。さて、4月号の問題は作図の問題です。
【問題】
一定の面積を持つ正方形があります。この正方形をもとにして、その面積の5倍の面積を持つ正方形を作図してください。作図は、定規とコンパスだけが使えます。また、作図に使った線は消さないでください。
ちなみに、1辺を5倍した正方形は面積比で52=5×5=25倍となってしまいます。私は次のように考えてみました。
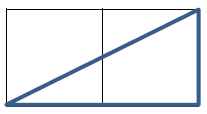
正方形を2つ並べると、面積が2倍の長方形が作れます。その長方形の対角線を引くと面積が半分になりますので、もとの面積と同じ面積の直角三角形が作れます。
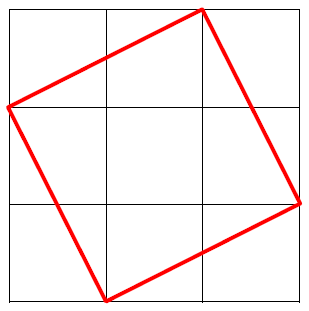
この直角三角形と、もとの面積と同じ面積の正方形をパズルのように組み合わせると、次のような正方形が作れます。
ここで
もとの正方形の面積を1とすると
面積1の直角三角形が4つあるので、1×4=4
中央に面積1の正方形があるので、1
よって、4+1=5となり5倍の面積の正方形となりました!
別解もありそうです。是非皆さんも考えてみてください。