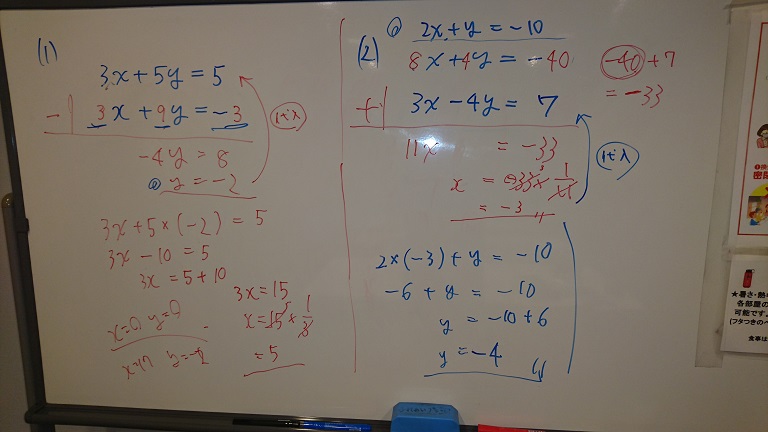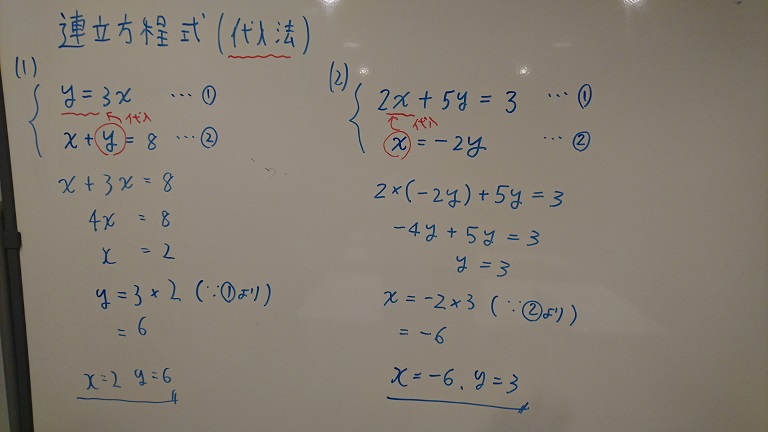
代入法
2つの方程式のうち、1つの式を変形して、もう一方の式に代入する方法です。こうすることで、文字が1種類だけになり方程式が解けるようになります。

次の連立方程式を代入法で解いてみよう!
\( \left\{ \begin{array}{l} y=3x \cdots ① \\ x+y=8 \cdots ② \end{array} \right. \)
①式を②式に代入すると
\(x+3x=8\)
\(4x=8\)
\(x=8\times \left(\dfrac{1}{4} \right)\)
\(x=2\)
これを①式に代入すると
\(y=3\times 2\)
\(y=6\)
\(\underline{x=2, y=-6}\)・・・(答)

解を求めたら、もとの方程式に代入して、答えがあっているか確認しましょう