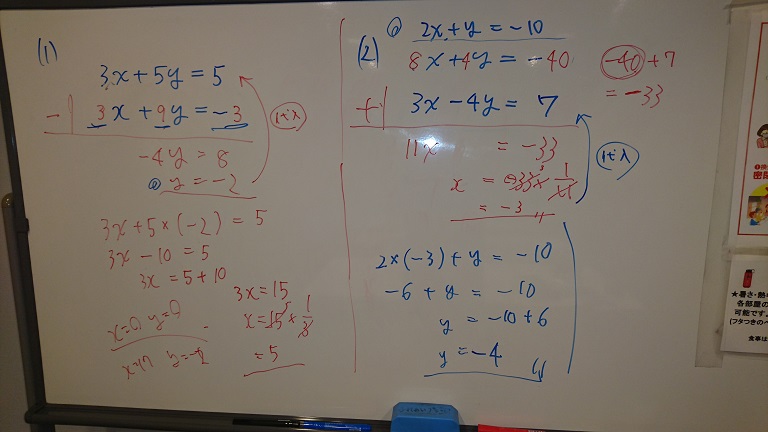
加減法
加減法は、2つの方程式の左辺どうし、右辺どうしを足したり、引いたりして、文字が1種類だけの方程式を作る解き方です。

次の連立方程式を加減法で解いてみよう!
\( \left\{ \begin{array}{l} 3x+5y=5 \cdots ① \\ x+3y=-1 \cdots ② \end{array} \right. \)
2式を引いて \(x\) を消去するために、文字の係数をそろえます。
②式を3倍すると
\( \left\{ \begin{array}{l} 3x+5y=5 \cdots ① \\ 3x+9y=-3 \cdots ② \end{array} \right. \)
\(3x+5y=5\)
-)\(\underline{3x+9y=-3}\)
\(-4y=8\)
\(y=8\times \left(- \dfrac{1}{4} \right) \)
\(y=-2\)
これを、①式に代入します。(②でもよいです)
\(3x+5\times (-2)=5\)
\(3x-10=5\)
\(3x=5+10\)
\(3x=15\)
\(x=5\)
\(\underline{x=5, y=-2}\)・・・(答)
\(x\) と \(y\) どちらを消去しても解くことができます。計算が楽な方を選びましょう。