昨日の問題の解答編です。別解で解けた方は是非教えてください。
まずは、問題の再掲。
四角形ABCDは正方形で、△EBCが正三角形であるとき、∠x を求めなさい。
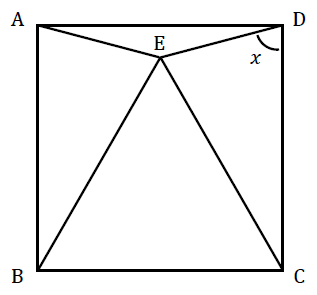
それでは、解答!
【解答】
△EBCは正三角形なので、三辺の長さは等しい。
したがって、CE=CB・・・①
また、四角形ABCDは正方形なので四辺の長さは等しい。
したがって、CB=CD・・・②
①, ②よりCE=CDであり、△CDEは二等辺三角形である。
ここで
∠ECB=60°より
∠DCE=90°ー 60°= 30°
ゆえに
∠x=(180°ー 30°)÷ 2 = 75°・・・(答)
正方形ABCDの一辺と正三角形EBCの一辺が等しくなるので、△CEDが二等辺三角形になることが分かれば簡単に解けますね。
そこに速く気づくようになるためには、たくさんの幾何の問題に触れて経験を積むことだと思います。