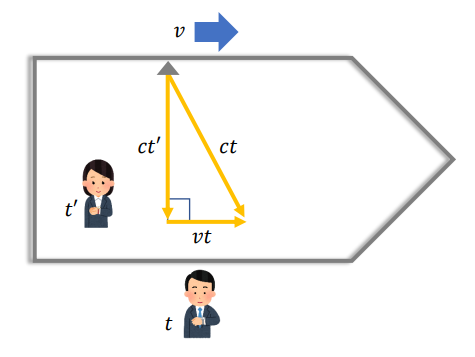
ローレンツ収縮に関する思考実験。
速度 \(v\) で移動する物体内で進行方向に垂直に光を放ちます。
ここで、物体の外の経過時間を \(t\)、物体の中の経過時間を \(t’\) とすると
縦の長さ \(ct’\)、横の長さ \(vt\)、斜辺の長さ \(ct\) となる直角三角形ができます。
三平方の定理より
\(\left(ct \right)^2=\left(ct’ \right)^2+\left(vt \right)^2\)
\(t’=t\sqrt{1-\left(\dfrac{v}{c} \right)^2}\)・・・①
物体の外からみて、進んだ距離 \(l\) を測定すると
\(l=vt\)・・・②
物体の中からみて、進んだ距離 \(l’\) を測定すると
\(l’=vt’\)・・・③
②, ③より
\(\dfrac{l}{l’}=\dfrac{vt}{vt’}=\dfrac{t}{t’}\)・・・④
①, ④より
\(l’=l\sqrt{1-\left(\dfrac{v}{c} \right)^2}\)
が得られます。この式より、\(l’\) は \(l\) より明らかに小さい。つまり、動いている物体内で距離を観測すると、その長さは収縮することになります。