新聞広告に2023年開成中学校の算数入試問題が掲載されていましたので、1問ご紹介。
是非、皆さんも挑戦してみてください。
※解答を見る前にまずは自分で考えてみることが大切です!
1 ウサギとカメが競争しました。
カメはスタート地点からゴール地点まで、毎分4mの速さで走り続けました。
ウサギはスタート地点をカメと同時に出発し、毎分60mの速さで走っていましたが、ゴール地点まで残り100mになったところで走るのをやめて、昼寝を始めました。昼寝を始めた60分後に目を覚ましたウサギは、カメに追い抜かれていることに気がつきました。あわてたウサギは、そこから毎分80mの速さでゴール地点まで走りましたが、ウサギがゴール地点に着いたのは、カメがゴール地点に着いた時刻の5秒後でした。
次の問いに答えなさい。
(1) ウサギが昼寝を始めてからカメがゴール地点に着くまでの時間は何分何秒ですか。
(2) ウサギが昼寝を始めたとき、ウサギはカメより何m先にいましたか。
(3) スタート地点からゴール地点までの道のりは何mですか。
百里を行く者は九十を半ばとす(戦国策)という故事があります。
“100里の距離を歩き通そうと思ったら、90里まで来たところで、やっと半分だと考える習慣が必要であること”の意で、ものごとは途中でしくじらないように最後まで気を引き締めて行わなければならない、ことを表しています。
解答は後日公開します!解いた方はコメントまで。
それでは解答編です!
【解答】
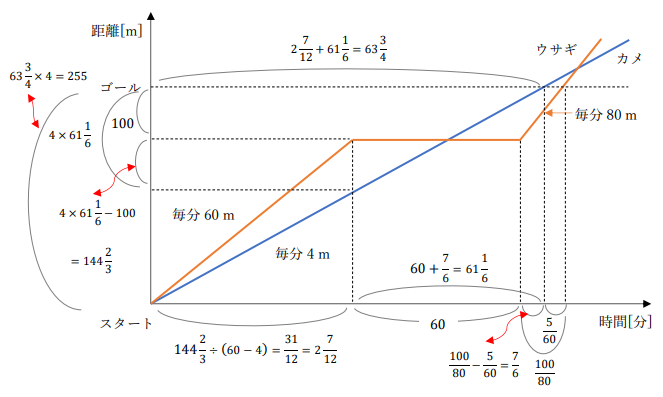
※ 略図です。実際にはカメのグラフの傾きはもっと小さくなります。
※ 5秒は分に単位変換します。1分は60秒なので、5秒⇒5÷60 分となります。
すると、求める距離や時間はグラフ上の長さになります。
→こうすることで、図形の問題にできる!
後は、分数の仮分数・帯分数に注意しながら計算を行います。この問題で利用する公式は(速さ)×(時間)=(距離)のみです。
(1)
\(60+\left(\dfrac{100}{80}-\dfrac{5}{60} \right)=60+\dfrac{7}{6}=61\dfrac{1}{6}\)
よって、61分10秒・・・(答)
(2)
\(4\times 61\dfrac{1}{6}-100=144\dfrac{2}{3}\) [m]・・・(答)
(3)
はじめ、ウサギとカメの速さの差が毎分 \(60-4=56\) m なので、\(144\dfrac{2}{3}\) m の差ができるまで
\(144\dfrac{2}{3}\div (60-4)=\dfrac{31}{12}=2\dfrac{7}{12}\) 分かかります。
したがって、カメがスタートからゴールするまでの時間は
\(1\dfrac{7}{12}+61\dfrac{1}{6}=63\dfrac{3}{4}\) 分となります。
よって、カメの速さは毎分4mなので
\(63\dfrac{3}{4}\times 4=255\) m ・・・(答)
文章題もグラフを書くことで、図形の問題にできるという良問でした。