「連続する3つの整数の和は, 3の倍数である」
このことを次のように説明した。
(説明)
連続する3つの整数のうち, もっとも小さい整数を \(n\) とすると, 連続する3つの整数は小さい順に \(n\), ア, イ と表すことができる。
ここで,
\(n + ( ア ) + ( イ ) = 3( ウ )\)
ウ は整数だから, \(3( ウ )\) は3の倍数である。
したがって, 連続する3つの整数の和は, 3の倍数である。
このとき, 上の ア ~ ウ に当てはまる式を, それぞれ求めなさい。
【解説】難度:易しい
連続する3つの整数は小さい順に
\(n\), \(n+1\), \(n+2\)
と表せるので
\(n + (n+1) + (n+2) = 3(n+1)\)
よって
ア:\(n+1\) イ:\(n+2\) ウ:\(n+1\)・・・(答)
(2)
太郎さんは庭に, 次の2つの条件1, 2を満たすような長方形の花だんを作ることにした。
(条件)
1 横の長さは, 縦の長さより5m長い。
2 花だんの面積は, 24 m2 である。
縦の長さを \(x\) m として方程式をつくると, 次のようになる。
\(ア = 24\)
したがって, この方程式を解くと, \(x= イ, ウ\) となる。
\(x= イ\) は, 縦の長さとして適していないから, 縦の長さは ウ m である。
このとき, 上の ア に当てはまる式を, イ, ウ には当てはまる数を, それぞれ書きなさい。
【解説】難度:易しい
縦の長さを \(x\) m とすると
横の長さは \(x+5\) m となる
花だんの面積が 24 m2 なので
\(x(x+5)=24\)
\(x^2+5x-24=0\)
\((x-3)(x+8)=0\)
\(x=-8, 3\)
\(x>0\) より \(x=3\)
よって、縦の長さは8m
ゆえに、ア:\(x(x+5)\) イ:\(-8\) ウ:\(3\)・・・(答)
(3)
下の図で, 点 A は関数 \(y=\frac{2}{x}\) と関数 \(y=ax^2\) のグラフの交点である。点 B は点 A を \(y\) 軸を対称移動させたものであり, \(x\) 座標は \(-1\) である。
このことから, \(a\) の値は ア であり, 関数 \(y=ax^2\) について, \(x\) の値が1から3まで増加するときの変化の割合は イ であることがわかる。
このとき, 上の ア , イ に当てはまる数を, それぞれ書きなさい。
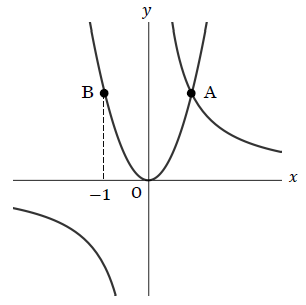
点 A の座標は \((1, 2)\) であるから
\(2=a\cdot 1^2\)
\(a=2\)
編かの割合は
\(\dfrac{y の増加量}{x の増加量}\) より
\(\dfrac{18-2}{3-1}=8\)
よって、ア:2 イ:8・・・(答)
(4)
陸上競技部の A さんと B さんは100m競争の選手である。下の図1, 図2は, 2人が最近1週間の練習でそれぞれ100mを18回走った記録をヒストグラムに表したものである。これらのヒストグラムをもとに, 次の1回でより速く走れそうな選手を1人選ぶとする。
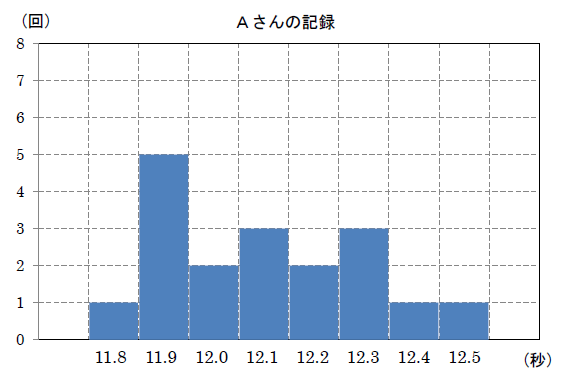
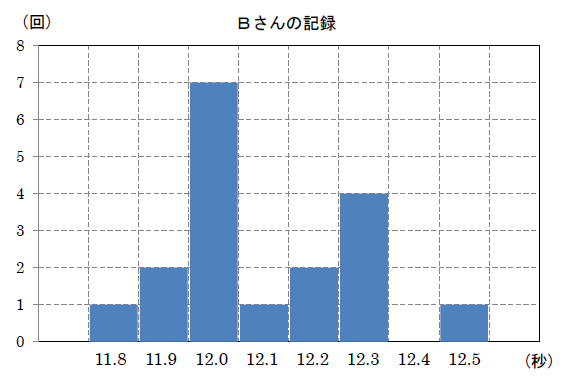
このとき, あなたならどちらの選手を選びますか。A さん, B さんのどちらか一方を選び, その理由を, 2人の中央値(メジアン)または最頻値(モード)を比較して説明しなさい。
【解説】難度:標準まず、A さんと B さんの記録の中央値と最頻値を求めます。
(i) A さん
中央値は \(12.1\) 秒
最頻値は \(11.9\) 秒
(ii) B さん
中央値は \(12.0\) 秒
最頻値は \(12.0\) 秒
問題文で2人の中央値または最頻値を比較して説明しなさい、とあるので
Aさんを選ぶ
(理由) Aさんの最頻値(11.9 秒)はBさんの最頻値(12.0 秒)よりも小さいから・・・(答)
Bさんを選ぶ
(理由) Bさんの中央値(12.0 秒)はAさんの中央値(12.1 秒)よりも小さいから・・・(答)