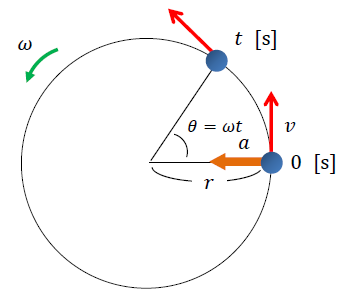
等速円運動の式を角速度 \(\omega\) から導出していきます。
角速度とは、円運動する物体が単位時間あたりに回転する角度のことです。
単位は、[rad/s]となるので
\(\omega =\dfrac{\theta}{t}\)・・・①
これが出発の式になります。
1sあたりに回転する弧の長さは \(r\omega\) なので 円の接線方向の速度 \(v\) [m/s] は
\(v=r\omega\)・・・②
となります。
等速円運動する物体が、円周を1周するのに要する時間を周期といいます。
周期 \(T\) [s] は
角度に着目すると、円1周の角度 \(2\pi\) を角速度 \(\omega\) で割ることで求まります。
また、円の長さに着目すると、円1周の長さ \(2\pi r\) を速さ \(v\) で割ることで求まります。
よって
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi r}{v}\)・・・③
となります。
物体が単位時間あたりに円周を回る回数を回転数といいます。 \(T\) の単位は[s/回] と表すことができるので、回転数 \(n\) は \(T\) の逆数をとって
\(n=\dfrac{1}{T}\) [回/s]・・・④
となります。
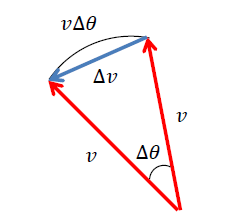
いよいよ加速 \(a\) を導出していきます。
加速度 \(a\) は
\(a=\dfrac{\Delta v}{\Delta t}\)
と定義されます。
ここで、\(\Delta \theta \rightarrow 0\) のとき
\(\Delta v=v\Delta \theta\) と近似して
\(a=\frac{v\Delta \theta}{\Delta t}=v\frac{\Delta \theta}{\Delta t}\)
\(=v\omega\)
\(=r\omega^2=\dfrac{v^2}{r}\) (∵②)・・・⑤
加速度の向きは、\(v\) に垂直、つまり円の中心を向きます。
角速度から等速円運動の式5つを導出しました。
暗記しておくことも大事ですが、忘れてもすぐ導けようにしておくことが重要です。