ボルツマン定数

ボルツマン定数とは

ボルツマン定数は気体の分子運動論で重要な定数の一つです。

ボルツマン定数は気体定数 $R$ をアボガドロ定数 $N_A$ で割ったもので、次のように求められます。

$k={\displaystyle \frac{R}{N_A}}={\displaystyle \frac{8.31}{6.02\times {10}^{23}}}\fallingdotseq 1.38\times {10}^{-23}$ J/K

ここで、気体分子の平均運動エネルギーを算出していきます。下記の導出の流れは大事です。

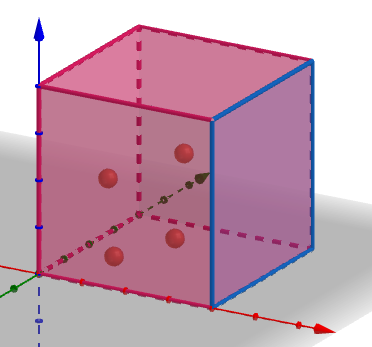
図のような１辺の長さ $L$ [m]、体積 $V=L^3$ [m³] の立方体の容器に、質量 $m$ [kg] の分子 $N$ 個からなる理想気体を入れます。このとき、分子は他の分子とは衝突せず等速直線運動し、壁との衝突は弾性衝突するものとします。

１回の衝突で壁Sが分子から受ける力積

壁Sに衝突する直前の分子の速度を $x$ 軸方向のみに着目し $v_x$ とすると、衝突後、分子の速度は $-v_x$ となるので、分子が壁から受ける力積は

$F\mathrm{\Delta }t=-v_X-v_x=-2v_x$

壁が分子から受ける力積は、作用・反作用の法則より $2m{v}_x$ [N・s]・・・① となります。

分子が壁Sと衝突するまでの時間

分子は $2L$ [m] ごとに壁Sと衝突するので、衝突の周期は

${\displaystyle \frac{2L}{v_x}}$ [s]・・・②

となります。

壁Sが１つの分子から受ける平均の力

時間 $t$ の間に分子が壁Sに衝突する回数は

$t÷{\displaystyle \frac{2L}{v_x}}={\displaystyle \frac{v_{x}t}{2L}}$ [回]（∵②）・・・③

であるから、時間 $t$ の間に壁Sが１つの分子から受ける力積は

$2m{v}_x\times {\displaystyle \frac{v_{x}t}{2L}}={\displaystyle \frac{m{v_x}^2}{L}}t$・・・④（∵①, ③）

となります。
したがって、時間 $t$ の間に壁Sが１つの分子から受ける平均の力の大きさ $f$ は

$f={\displaystyle \frac{m{v_x}^2}{L}}$・・・⑤（∵④）

となります。

壁Sが $N$ 個の分子から受ける圧力

壁Sが $N$ 個の分子から受ける平均の力の大きさは、$v_x$ の平均を $\overline{v_x}$ とすると⑤より

$F=N\times {\displaystyle \frac{m\overline{{v_x}^2}}{L}}={\displaystyle \frac{Nm\overline{{v_x}^2}}{L}}$・・・⑥（∵⑤）

したがって、気体の圧力 $p$ は

$p={\displaystyle \frac{F}{L^2}}={\displaystyle \frac{Nm\overline{{v_x}^2}}{L^3}}={\displaystyle \frac{Nm\overline{{v_x}^2}}{V}}$・・・⑦

ここで、

$\overline{v^2}=\overline{{v_x}^2}+\overline{{v_y}^2}+\overline{{v_z}^2}$

であり、分子の運動はどの方向にも均等で偏りがないと考えると、

$\overline{{v_x}^2}=\overline{{v_y}^2}=\overline{{v_z}^2}$

よって、$\overline{{v_x}^2}={\displaystyle \frac{\overline{v^2}}{3}}$・・・⑧

⑦, ⑧より

$p={\displaystyle \frac{Nm\overline{v^2}}{3V}}$

$pV={\displaystyle \frac{Nm\overline{v^2}}{3}}$

ここで、気体の状態方程式 $pV=nRT$ より

${\displaystyle \frac{Nm\overline{v^2}}{3}}=nRT$

ゆえに、理想気体の分子１個あたりの運動エネルギーは

${\displaystyle \frac{1}{2}}m\overline{v^2}={\displaystyle \frac{3}{2}}{\displaystyle \frac{nRT}{N}}$

$N=n{N}_A$ であるから、

${\displaystyle \frac{1}{2}}m\overline{v^2}={\displaystyle \frac{3}{2}}{\displaystyle \frac{nRT}{n{N}_A}}={\displaystyle \frac{3}{2}}{\displaystyle \frac{R}{N_A}}T$

ここで、$k={\displaystyle \frac{R}{N_A}}$（ボルツマン定数） と置くと

${\displaystyle \frac{1}{2}}m\overline{v^2}={\displaystyle \frac{3}{2}}kT$・・・⑨

⑨式より、理想気体の分子の平均の運動エネルギーは、分子の種類によらず絶対温度 $T$ によって決まることが導出できました。