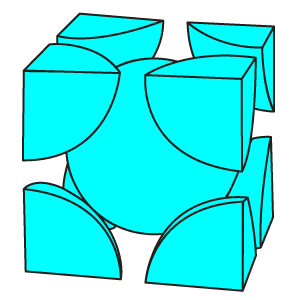
現在、精密なアボガドロ定数の測定はシリコン(Si)の結晶を用いて測定されています。
この値に基づいてファラデー定数などの物理、化学における種々の定数が定められているため、アボガドロ定数はとても重要な定数です。
ここで、鉄の結晶構造からアボガドロ定数を算出してみたいと思います。
まず、鉄の結晶格子は体心立方格子なので、単位格子に含まれる原子の数は2となります。
次に、単位格子の1辺の長さを求めます。Wikipediaによると鉄の原子半径は、126pm なので
126 pm → 126×10-12 m → 126×10-10 cm
体心立方格子の一辺の長さ( \(l\) )と原子半径( \(r\) )の関係は
\(r=\dfrac{\sqrt{3}}{4}l\) なので
\(l=\dfrac{4}{\sqrt{3}}r\)
\(\sqrt{3}\fallingdotseq 1.73\) とすると
\(l=\dfrac{4}{1.73}\times 126\times 10^{-10}\)
\(\fallingdotseq 2.91\times 10^{-8}\) [cm] となります。
鉄の密度は \(7.874\) [g/cm3] より、鉄の単位格子中の質量は
\(\left(2.91\times 10^{-8} \right)^3\times 7.874 \)
\(=1.94\times 10^{-22}\) [g]
鉄の原子量 Fe=56 よりアボガドロ定数 \(N_A\) は次のように計算できます。
\(N_A =\dfrac{2}{\dfrac{1.94\times 10^{-22}}{56}}\)
\(=5.8\times 10^{23}\) [/mol]
近い数値がでました。鉄以外の金属でも、アボガドロ定数の算出を試してみると面白いかもしれません。