問題
点 \((5, 3)\) を点 \((1, 1)\) のまわりに \(\dfrac{\pi}{6}\) だけ回転した点の座標を求めなさい。
【解答】
まずは、三角関数とベクトルを利用した解法です。
図のように、\(A(1, 1)\), \(B(5, 3)\), \(C(5, 1)\), 回転した点を \(B’\), \(\angle BAC=\theta\) とします。
点 \(B’\) の座標は
\(\overrightarrow{OB’}=\overrightarrow{OA}+\overrightarrow{AB’}\)・・・①
と表せます。
まずは、三角関数とベクトルを利用した解法です。
図のように、\(A(1, 1)\), \(B(5, 3)\), \(C(5, 1)\), 回転した点を \(B’\), \(\angle BAC=\theta\) とします。
点 \(B’\) の座標は
\(\overrightarrow{OB’}=\overrightarrow{OA}+\overrightarrow{AB’}\)・・・①
と表せます。
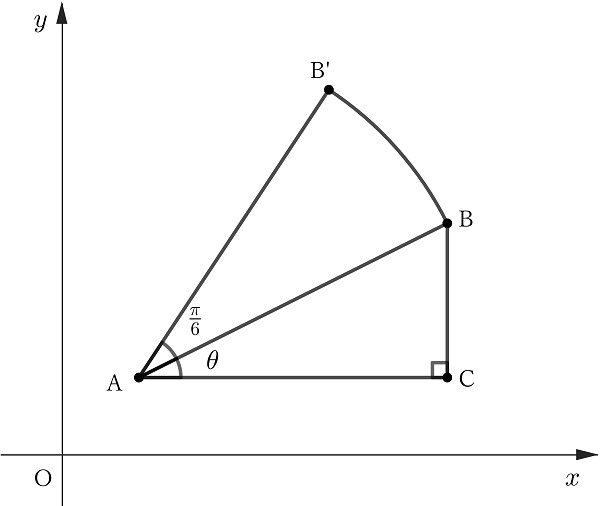
したがって
\(\cos{\theta}=\dfrac{4}{2\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)・・・②
\(\sin{\theta}=\dfrac{2}{2\sqrt{5}}=\dfrac{1}{\sqrt{5}}\)・・・③
なので
\(\overrightarrow{AB’}\)
\(=\left( 2\sqrt{5} \cos \left( \theta + \dfrac{\pi}{6} \right), 2\sqrt{5} \sin \left( \theta + \dfrac{\pi}{6} \right) \right)\)
\(2\sqrt{5} \cos \left( \theta + \dfrac{\pi}{6} \right)\)
\(=2\sqrt{5} \left( \cos \theta \cos \dfrac{\pi}{6} – \sin \theta \sin \dfrac{\pi}{6} \right)\) (∵加法定理)
\(=2\sqrt{5} \left( \dfrac{2}{\sqrt{5}} \cdot \dfrac{\sqrt{3}}{2} – \dfrac{1}{\sqrt{5}} \cdot \dfrac{1}{2} \right)\) (∵②, ③)
\(=2\sqrt{3}-1\)
同様に
\(2\sqrt{5} \sin \left( \theta + \dfrac{\pi}{6} \right)\)
\(=2+\sqrt{3}\)
したがって
\(\overrightarrow{AB’}=\left(2\sqrt{3}-1, 2+\sqrt{3}\right)\)・・・④
よって、①, ④より
\(\overrightarrow{OB’}=(1, 1)+\left(2\sqrt{3}-1, 2+\sqrt{3}\right) \)
\(=(2\sqrt{3}, 3+\sqrt{3})\)・・・(答)
算出まで、加法定理など計算量が多いですね。では、複素数を利用した”省エネ”な解法です!
【別解】
\(A=1+i\), \(B=5+3i\) とおくと
\((B-A)\left(\cos \dfrac{\pi}{6} + i \sin \dfrac{\pi}{6} \right)=B’-A\)
\((4+2i)\left( \dfrac{\sqrt{3}}{2} + \dfrac{1}{2} i\right)=B’-(1+i)\)
\(B’=2\sqrt{3}+\left(3+\sqrt{3}\right)i\)
よって、\(B’\) の座標は
\(\left(2\sqrt{3} , 3+\sqrt{3} \right)\)・・・(答)
簡単に解答できました!「三角関数+ベクトル」の解法と比べてみてください。