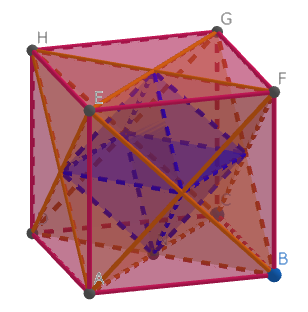
図のような立方体ABCD-EFGHについて、4点A,C,F,Hを頂点とする四面体を S とし、4点B,D,E,Gを頂点とする四面体をT とします。
S とT の共通部分の立体Uはどのような立方体になるでしょうか?
Geogebraで立体の作図をしてみると、正八面体であることがすぐに分かります。
紙ベースの試験で正八面体と答えるのは難しそう・・・。
では、問題です。
立体U の体積は立方体ABCD-EFGHの何倍となるでしょうか?
答えはコメント欄にどうぞ!
立方体の1辺の長さを \(2a\) とすると、立方体の体積 \(V\) は
\(V=2a\times 2a\times 2a=8a^3\)・・・①
正四面体の1辺の長さは、三平方の定理より \(\sqrt{2} a\) なので、正四面体の体積 \(V’\) は
\(V’=\sqrt{2}a\times \sqrt{2}a\times a \times \dfrac{1}{3}\times 2=\dfrac{4}{3}a^3\)・・・②
①, ②より
\(\dfrac{V’}{V}=\dfrac{1}{6}\)・・・(答)