年末の高校県立入試向け実力テストで正答率が1%だった問題です。(解くのに時間がかかると判断したためか皆さん敬遠してしまったのかもしれません)是非皆さんチャレンジしてみてください。解答は後日発表します。※ 解けた方はコメント欄にどうぞ。
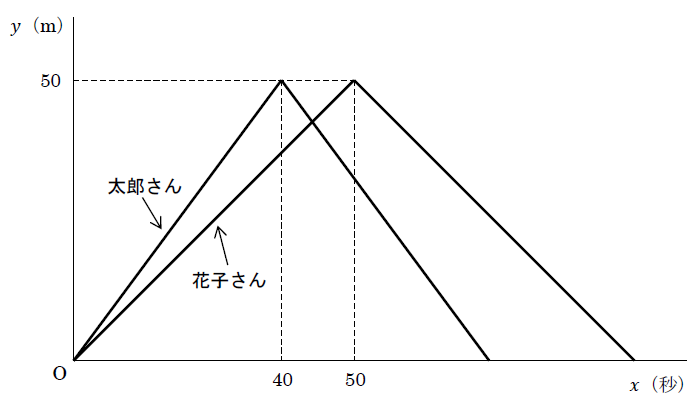
コースの長さが50mのプールがあります。太郎さんと花子さんが、このコースを同じ方向に同時にスタートし50mで折り返してそれぞれ100m泳ぎました。図は、スタートしてからx秒後のスタート地点からの距離をymとして、xとyの関係をグラフに表したものです。
コース上に地点Pがあり、太郎さんがコースを折り返して地点Pを通過した13秒後に、同じくコースを折り返した花子さんが地点Pを通過しました。地点Pはスタート地点から何mのところにあるか求めなさい。
ただし、太郎さんと花子さんはそれぞれ一定の速さで泳いだものとします。
それでは、解答を発表します!(2023.1.2)
【解答1】
グラフより、太郎さんと花子さんの速さを求めると
太郎さん・・・\(\dfrac{5}{4}\) [m/s]
花子さん・・・\(1\) [m/s]
となります。 求める地点Pのスタート地点からの距離を \(y\) [m]とすると
太郎さんは、折り返して地点Pを通過するまでに
\(\dfrac{100-y}{\frac{5}{4}}=\dfrac{4(100-y)}{5}\) 秒かかるので、 その13秒後は
\(\dfrac{4(100-y)}{5}+13\) 秒
花子さんの速さは\(1\) [m/s] なので
\(1\times \left\{\dfrac{4(100-y)}{5}+13\right\}=100-y\)
これを \(y\) について解くと
\(y=35\) [m]・・・(答)
【解答2】
つくばっこさんより投稿頂いた相似を利用した解答です。
グラフを図形と考えて相似から考えることがポイントです。
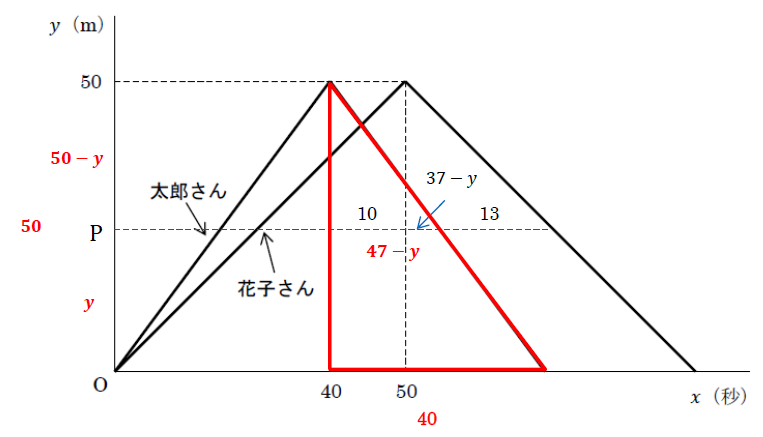
\(40:(47-y)=50:(50-y)\)
\(50(47-y)=40(50-y)\)
\(y=35\) [m]・・・(答)





初めまして!
子どもに見せて解いてもらったところ二通りの解き方ができました。
答え 35m
・それぞれの速さから、13秒差がつくまでの時間を求め、そこから距離を求める。(小6)
・グラフを図形と考えて相似から考える。(中1)
つくばっこさん
解答の投稿ありがとうございました!正解です!
2通りの解法で解けてすごいです。
投稿頂いた解法は解答を作成する際に参考にさせて頂きました。
やったー! 正解だー!
ありがとうございます!