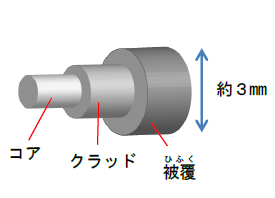
光ファイバーは、石英ガラスまたはプラスチックで作られた人工的な繊維で光通信などに利用されています。
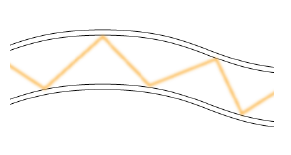
クラッドよりもコアの屈折率を高くすることで、ケーブルが少しくらい曲がっても光は繊維の中を全反射しながら進むことができます。
例題
空気の屈折率を1、コアの屈折率を n1、クラッドの屈折率を n2 (1<n2<n1)とするとき、コアの中心軸になす角θ (0<θ<\(\frac{\pi}{2}\)) で入射させた光が、コアとクラッドとの境界面で全反射を繰り返しながら進むための条件を n1とn2の間に成り立つ不等式で表しなさい。

【解答】
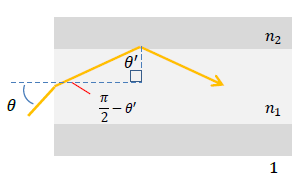
臨界角をθ0 とすると屈折の法則より
\(n_1 \sin{\theta_0}=n_2 \sin{\frac{\pi}{2}}=n_2\)
\(\sin{\theta}=n_1 \sin\left({\frac{\pi}{2}-\theta’}\right)=n_1 \cos{\theta’}\)
\(=n_1 \sqrt{1-\sin ^2 \theta’}\)
\(< n_1 \sqrt{1-\frac{n_2 ^2}{n_1 ^2}}=\sqrt{n_1 ^2 -n_2 ^2}\)
よって、\(\sin{\theta}<\sqrt{n_1 ^2 - n_2 ^2}\)
\(n_1 \sin{\theta_0}=n_2 \sin{\frac{\pi}{2}}=n_2\)
\(\sin{\theta}=n_1 \sin\left({\frac{\pi}{2}-\theta’}\right)=n_1 \cos{\theta’}\)
\(=n_1 \sqrt{1-\sin ^2 \theta’}\)
\(< n_1 \sqrt{1-\frac{n_2 ^2}{n_1 ^2}}=\sqrt{n_1 ^2 -n_2 ^2}\)
よって、\(\sin{\theta}<\sqrt{n_1 ^2 - n_2 ^2}\)
ゆえに、\(\sqrt{n_1 ^2 -n_2 ^2}>1\) であれば上の式を常に満たす。・・・(答)





