今日の授業(中3数学)は接弦定理の証明に挑戦しました。
円周角の定理を理解することで、そこから派生した定理も理解することができます。
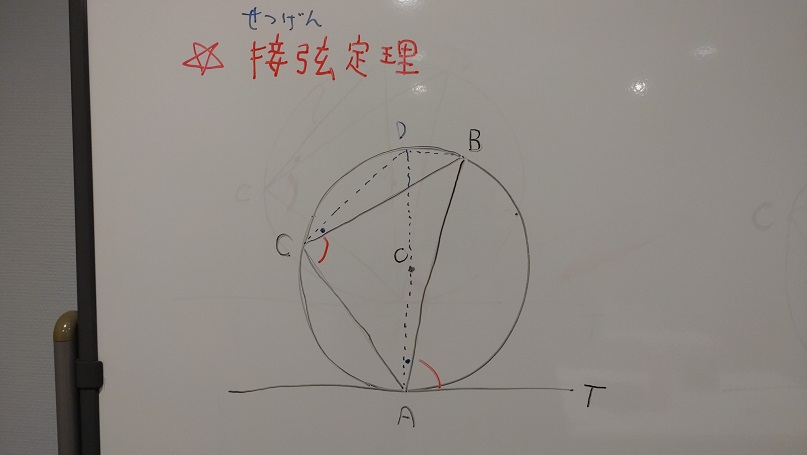
接弦定理
円の接線とその接点を通る弦のつくる角は、その角の内部にある弧に対する円周角に等しい。
これは、図で \(\angle BAT = \angle ACB\) となることを意味しています。
証明のポイントは、直径ADとなる補助線を引くことです。
\(\angle DAT =\angle DCA=90°\)
円周角の定理より
\(\angle DAB=\angle DCB\)
\(\angle BAT=\angle DAT – \angle DAB\)
\(\angle ACB=\angle DCA – \angle DCB\)
よって、\(\angle BAT = \angle ACB\)・・・(証明終)