円周角の定理

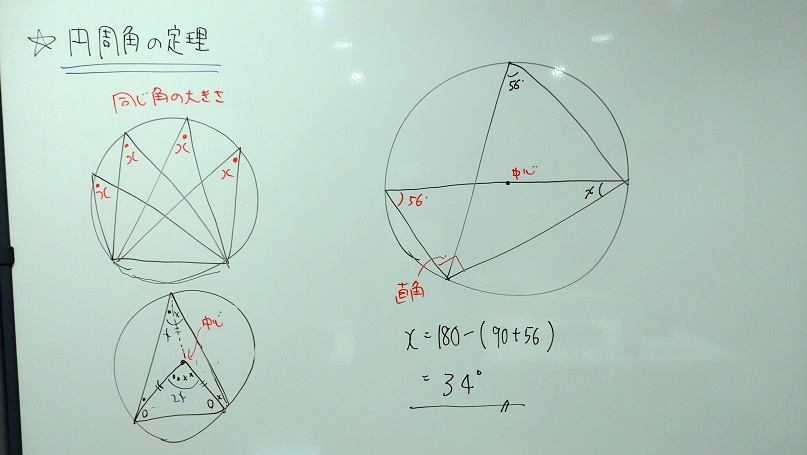
本日の授業（中３数学）は、円周角の定理についてでした。

円周角の定理

---

【円周角の定理】
[1] １つの弧に対する円周角の大きさは、その弧に対する中心角の大きさの半分である。
[2] 同じ弧に対する円周角の大きさは等しい。

---

図のように、直径 \(PC\) を引き \(\angle APO=a\), \(\angle BPO=b\) とします。
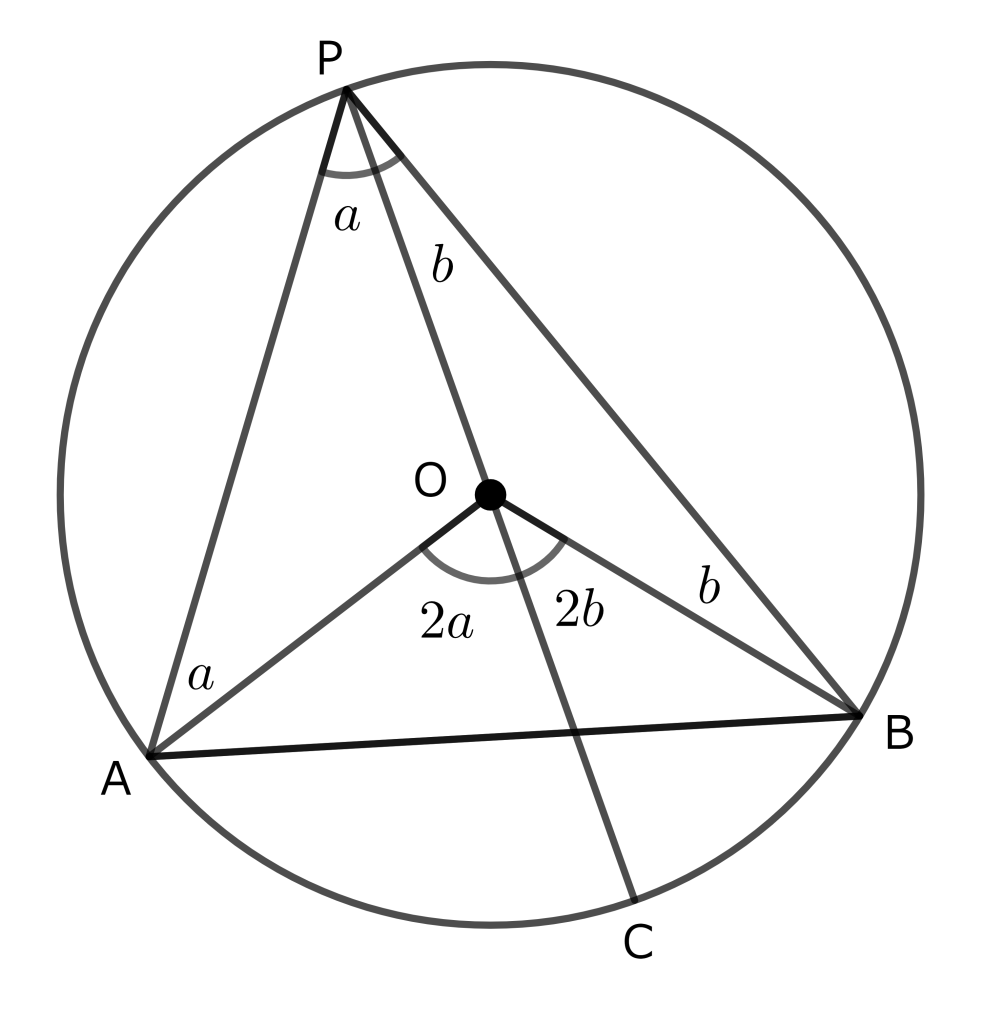
半径は等しいことから、△\(OPA\) は二等辺三角形となるので
\(\angle APO=\angle PAO= a\)
\(\angle AOC\) は外角なので \(\angle AOC=2a\)
同様に、\(\angle BOC=2b\)

よって
\(\angle AOB=\angle AOC + \angle BOC\)
\(=2a+2b\)
\(=2(a+b)\)

\(\angle APB=a+b\) なので
\(\angle APB=\dfrac{1}{2} \angle AOB\)
となります。

同じ弧に対する円周角に対し、中心角は１つに決まりますので、「定理[2] 同じ弧に対する円周角の大きさは等しい」ことも分かります。

一度は自分で証明しておくことで、定理の理解が深まります。
是非、証明してみてください。