新学年になり、学校で新しい教科書も配布されました。装いも新たに新年度も頑張りましょう!
中学3年生は、中学最終学年であり、いよいよ受験生です。部活の大会や修学旅行といった行事、実力テストなど多忙なスケジュールですが、是非とも悔いのない一年を過ごして頂きたいです。
今日は新中3・数学「展開」についてです。
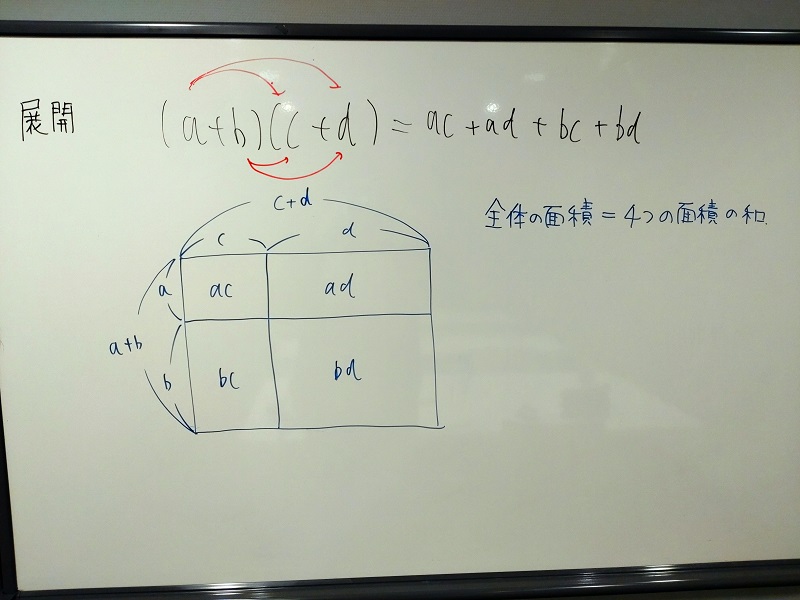
展開公式 \((a+b)(c+d)=ac+ad+bc+bd\)
は、面積で考えると理解しやすいです。
全体の面積 = \((a+b)(c+d)\)・・・①
各面積の和 = \(ac+ad+bc+bd\)・・・②
と表せます。
全体の面積 = 各面積の和 より
(\(a+b)(c+d)=ac+ad+bc+bd\) (∵ ①=②)
を導くことができます。
この公式を利用して、次の展開公式も導くことができます。
展開の公式
[1] \((x+a)(x+b)=x^2+(a+b)x+ab\)[2] \((x+a)^2=x^2+2ax+a^2\)
[3] \((x-a)^2=x^2-2ax+a^2\)
[4] \((x+a)(x-a)=x^2-a^2\)
これらの公式は、(左辺)=(右辺)となることを示すことで証明することができます。
展開の公式[4]を例にすると
(左辺)\(=(x+a)(x-a)\)
\(=x^2-ax+ax-a^2\)
\(=x^2-a^2=\)(右辺)
となって、展開の公式[4]が示されました。
[1]~[3]も同様です。是非、皆さんも公式を実際に証明してみてください。
\(a, b\) が具体的な数値による展開は練習あるのみです!