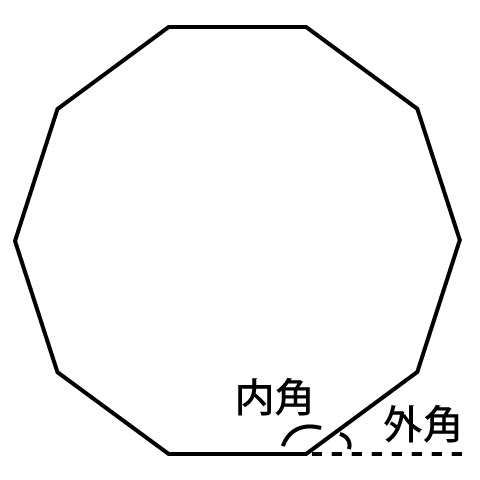
多角形の角について、次の公式があります。
\(n\) 角形の
(内角の和)\(=180(n-2)\)・・・(i)
(外角の和)\(=360\)・・・(ii)
(i)式について
\(n\) 角形内に \(n-2\) 個の三角形がつくれるので
三角形の内角の和が180°であることから
\((n-2)\times 180=180(n-2)\)
(ii)式について
内角と外角の和は180°であるので
(内角の和)+(外角の和)\(=180n\)
\(180(n-2)\) +(外角の和)\(=180n\)
\(180n-360\) +(外角の和)\(=180n\)
(外角の和)\(=360\)
ということで(ii)式も導けました。