水中の物体は浮き上がって見えます。
では、どのくらい浮き上がっているのでしょうか?
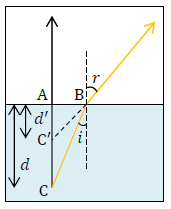
水中の物体を真上から観察すると物体の光は直進します。
真上からわずかにずれると、光は屈折します。真上から見た光の直線と屈折して空気中に出た光の直線の交点が浮き上がって見える物体の位置となります。
空気の屈折率を1、水の屈折率を \(n\)として
屈折の法則より
\(n\sin{i}=\sin{r}\)・・・①
\(AB=d\tan{i}\)・・・②
\(AB=d’\tan{r}\)・・・③
②, ③より
\(d\tan{i}=d’\tan{r}\)・・・④
真上からわずかにずれて観察しているので
角 \(i, r\) はきわめて小さく
\(\tan{i}=\sin{i}\)
\(\tan{r}=\tan{r}\)
と近似できる。
したがって、④は
\(d\sin{i}=d’\sin{r}\)
\(d’=\dfrac{\sin{i}}{\sin{r}}d\)
\(=\dfrac{d}{n}\) (①より)
水の屈折率は、約1.33ですので、水中1mにある物体は水面から見ると
\(\dfrac{1}{1.33}\fallingdotseq 0.75\)
つまり、0.75m下にあるように見えるというわけです。





