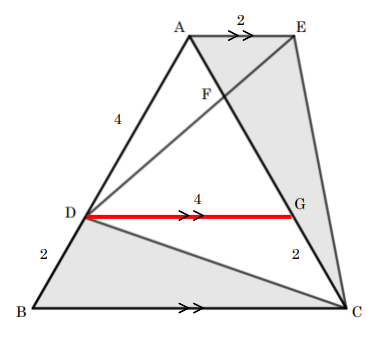
下の図１は, 三角すいの展開図であり, AB=12cm, AC=9cm, ED=5cm である。
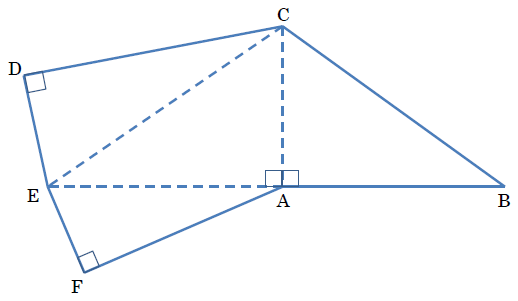
(太郎さんと花子さんの会話)
太郎：辺ABと辺ACの長さがわかっているから, 三角形ABCの面積は簡単に求めることができるよ。他の三角形の面積も求めることができるかな。
花子：辺EDの長さが5cmだから, 三角形CDEの面積もわかりそうね。
太郎：確かにそうだね。三角形CDEの面積は（ ア ）cm2 になるよ。
花子：次は, この展開図を組み立てて体積について考えてみましょう。
太郎：どの面を底面としてみると体積が求めやすいかな。
花子：組み立てたときに頂点が重なるところがあるので, 図２のように展開図に（面あ）, （面い）, （面う）, （面え） と名前をつけて考えてみると, （面え）を三角すいの底面とするといいかもしれないわね。
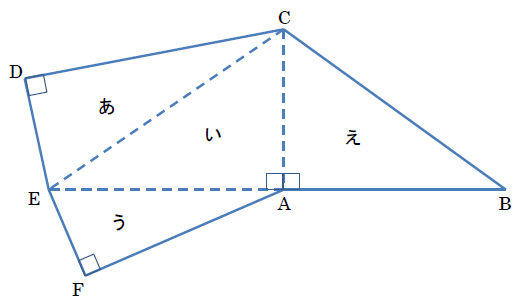
花子：これで体積を求めることができうそうね。
太郎：計算してみたら, 三角すいの体積は（ ウ ）cm3 になるよ。
花子：ところで, 底面とする面を変えてみると, 三角すいの高さが変わるわね。
太郎：なるほど。そうすると, 三角すいの高さが, 一番高くなるのは（ エ ）を底面にしたときで, 一番低くなるのは（ オ ）を底面にしたときだよ。
(1) 会話中の（ ア ）に当てはまる数を求めなさい。
(2) 会話中の（ イ ）に当てはまる面を, （面あ）～（面う）の中からすべて選んで, その記号を書きなさい。また, （ ウ ）に当てはまる数を求めなさい。
(3) 会話中の（ エ ）, （ オ ）に当てはまる面を, （面あ）～（面え）の中から一つ選んで, その記号をそれぞれ書きなさい。
【解説】難度：標準
(1) AB=12cm, AC=9cm より
三平方の定理よりBC=15cm
また, CD=BC=15cm より
三角形CDEの面積は
\(\dfrac{1}{2}\cdot 5\cdot 15=\dfrac{75}{2}\) cm2・・・(答)
(2) （イ）は（面あ）, （面う）・・・(答)
底面（面え）の面積は \(\dfrac{1}{2}\cdot 12\cdot 9=54\) cm2
高さはED=5cm
よって体積は \(\dfrac{1}{3}\cdot 54\cdot 5=90\)・・・(答)
(3) 三角すいの高さが一番高くなるのは底面積が一番小さいとき
高さが一番低くなるのは底面積が一番大きいとき
なので, それぞれの面の面積を求めると
（あ）⇒ \(\dfrac{75}{2}\) cm2
（い）⇒ \(\dfrac{117}{2}\) cm2
（う）⇒ 30 cm2
（え）⇒ 54 cm2
したがって
（え）は（う）, （お）は（い）・・・(答)
