H市の工場では, 2種類の燃料A, Bを同時に使って, ある製品を作っている。燃料A, Bはそれぞれ一定の割合で消費され, 燃料Aについては, 1時間あたり30L消費される。また, この工場では, 燃料自動補給装置を導入して, 無人で長時間の自動運転を可能にしている。この装置は, 燃料A, Bの残量がそれぞれ200Lになると, ただちに, 15時間一定の割合で燃料を補給するようんに設定されている。
下の図は, 燃料A, Bについて「ある時刻」から \(x\) 時間後の燃料の残量を \(y\) Lとして, 「ある時刻」から80時間後までの \(x\) と \(y\) の関係をグラフに表したものである。
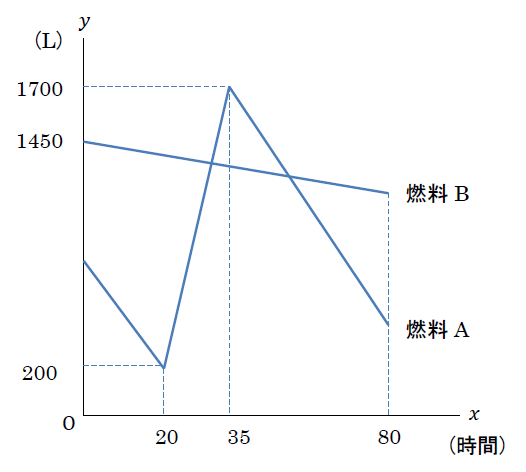
(1) 「ある時刻」の燃料Aの残量は何Lであったか求めなさい。
(2) 「ある時刻」の20時間後から35時間後までの間に, 燃料Aは1時間あたり何L補給されていたか求めなさい。
(3) 「ある時刻」から80時間後に燃料A, Bの残量を確認したところ, 燃料Aの残量は燃料Bの残量より700L少なかった。
このとき, 燃料Bが「ある時刻」から初めて補給されるのは「ある時刻」から何時間後か求めなさい。

問題文が長いときは状況を正しく読みとろう
(1) 20時間経って燃料Aの残量は200Lだから, 「ある時刻」に燃料Aは
30×20+200=800Lであった。・・・(答)
(2) 消費される分も補給されているので
\(\dfrac{(1700-200)+30\times(35-20)}{35-20}=130\) L補給されていた。・・・(答)
(3) 80時間後の燃料Aの残量は, 1700-30×(80-35)=350L
つまり, このときの燃料Bの残量は, 350+700=1050L
よって, 燃料Bは1時間あたり \(\dfrac{1450-1050}{80}=5\) L消費する。ゆえに, 燃料Bが「ある時刻」から初めて補給されるのは
\(\dfrac{1450-200}{5}=250\) 時間後となる。・・・(答)

燃料は消費されながら補給されることに注意だね