茨城県立高校入試 数学１ 解説

(1)
　A, B, C, D の４つのチームが自分のチーム以外のすべてのチームと試合を行った。下の表は、その結果をまとめたものである。得失点差とは, 得点合計から失点合計をひいた値である。
　このとき, 下の ア に当てはまる数を求めなさい。

表
【解説】難度：易しい
問題文に、「得失点差とは, 得点合計から失点合計をひいた値である。」とあるので
ア $=3-7=-4$・・・(答)
A, C, D チームも同様の計算ルールで得失点差の値が求められていることが分かります。

---

(2)
　下の図のように, 長方形 ABCD の中に１辺の長さが $\sqrt{5}$ m と $\sqrt{10}$ m の正方形がある。
　このとき, 斜線部分の長方形の周の長さを求めなさい。

【解説】難度：易しい
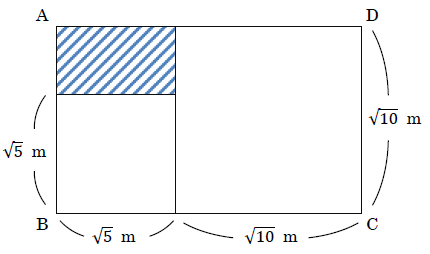
斜線部の長方形の縦の長さは $\sqrt{10}-\sqrt{5}$
横の長さは $\sqrt{5}$
なので、周の長さは
$2(\sqrt{10}-\sqrt{5})+2\sqrt{5}$
$=2\sqrt{10}$・・・(答)

---

(3)
　1000円で, １個 $a$ 円のクリームパン５個と１個 $b$ 円のジャムパン３個を買うことができる。ただし, 消費税は考えないものとする。
　この数量関係を表した不等式としてもっとも適切なものを, 次のア～エの中から一つ選んで, その記号を書きなさい。

ア　$1000-(5a+3b)<0$
イ　$5a+3b<1000$
ウ　$1000–(5a+3b)\geqq 0$
エ　$5a+3b\geqq 1000$

【解説】難度：易しい
１個 $a$ 円のクリームパン５個と１個 $b$ 円のジャムパン３個
の料金は $5a+3b$ 円
この金額が1000円以下であれば良いので
$5a+3b\leqq 1000$
$1000–(5a+3b)\geqq 0$
よって、ウ・・・(答)

---

(4)
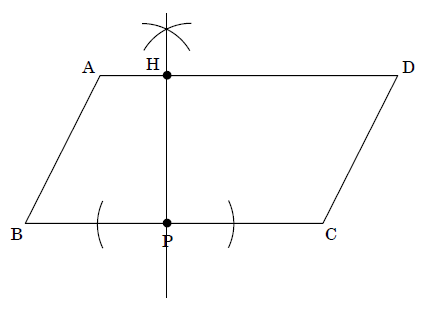
　花子さんは, 下の図の平行四辺形 ABCD の面積を求めるために, 辺 BC を底辺とみて, 高さを測ろうと考えた。
　点 P を下の図のようにとるとき, 線分 PH が高さとなるような点 H を作図によって求めなさい。
　ただし, 作図に用いた線は消さずに残しておくこと。

【解答】難度：易しい
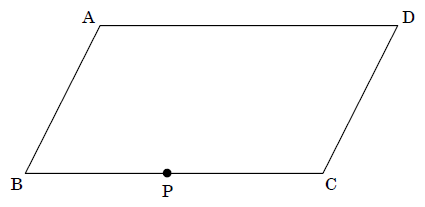
点 P を通り、線分 BCに垂直な直線を作図する。その直線と線分 AD の交点を点 D とすれば良い。