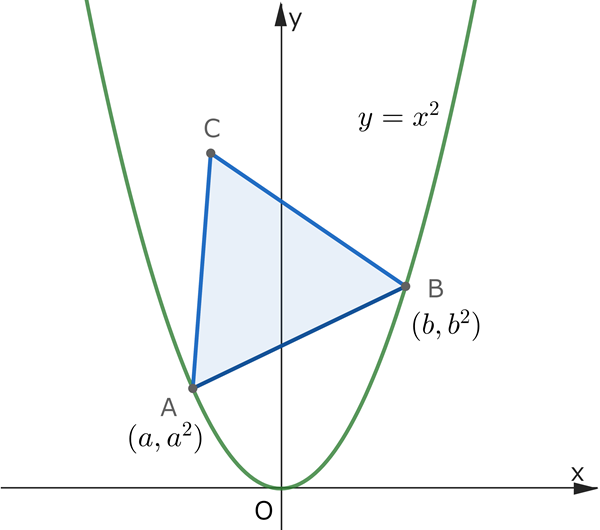
12/16 の問題の解答編です!
別解があったら是非教えてください。まずは問題を再掲。問題を解いていない方は、自分で問題を解いてから解答編を見ると学習に効果的です。
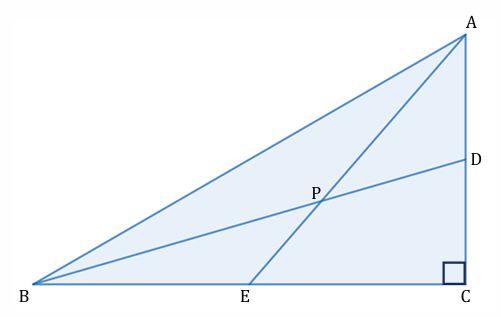
【問題】
図ような、AB = 12 cm、∠ACB = 90°、∠BAC = 60° である直角三角形 ABC があります。辺 AC 、辺 BC の中点をそれぞれ D、E とし、線分 AE と線分 BD の交点を P とします。このとき、線分 BP の長さを求めなさい。
図ような、AB = 12 cm、∠ACB = 90°、∠BAC = 60° である直角三角形 ABC があります。辺 AC 、辺 BC の中点をそれぞれ D、E とし、線分 AE と線分 BD の交点を P とします。このとき、線分 BP の長さを求めなさい。
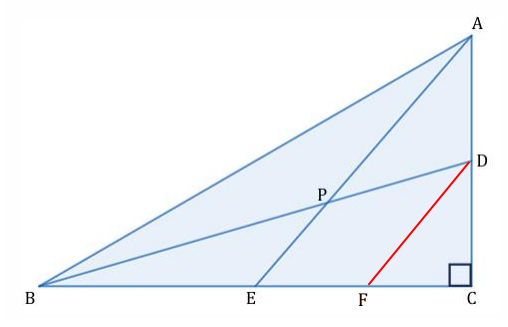
【解答】
点 D を通り、線分 AE に平行な線を引くと
点 D は線分 AC の中点なので、点 F は線分 EC の中点となる。
BE:EF=BP:PD
BE:EF=2:1
より、BP:PD=2:1
CD=3 cm、BC=\(6\sqrt{3}\) cm
三平方の定理より
BD=\(3\sqrt{13}\) cm
よって、BP=\(\dfrac{2}{3}\times 3\sqrt{13}\)
=\(2\sqrt{13}\) cm・・・(答)
点 D を通り、線分 AE に平行な線を引くと
点 D は線分 AC の中点なので、点 F は線分 EC の中点となる。
BE:EF=BP:PD
BE:EF=2:1
より、BP:PD=2:1
CD=3 cm、BC=\(6\sqrt{3}\) cm
三平方の定理より
BD=\(3\sqrt{13}\) cm
よって、BP=\(\dfrac{2}{3}\times 3\sqrt{13}\)
=\(2\sqrt{13}\) cm・・・(答)
高校の内容まで進んだ方はベクトルで解いてみると面白いですよ!