本日の中3数学の指導は、「正多角形の内角・外角」を求める問題です。
\(n\) 角形の内角の和は
\(180\times (n-2)\)
なので、正多角形の1つの内角の大きさは
\(\dfrac{180\times (n-2)}{n}\)
となります。
ちなみに、\(n\) 角形の外角の和は
\(180n-180\times (n-2)=360\)
で常に \(360°\) になります。
【問題】
正十角形の1つの内角の大きさを求めなさい。
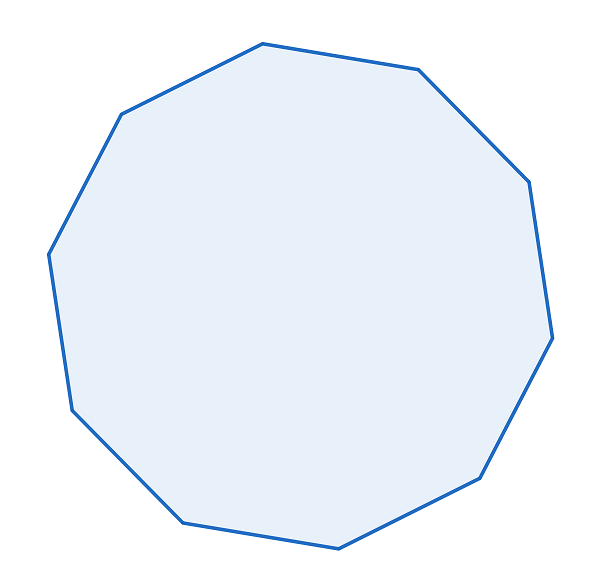
【解答】
\(\dfrac{180\times (10-2)}{10}\)
\(=144°\)・・・(答)
【別解】
1つの外角の大きさは
\(\dfrac{360}{10}=36\)
\(180-36=144°\)・・・(答)