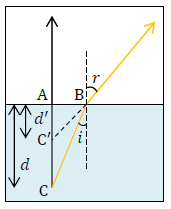
斜方投射で遠方までボールを投げるためには、45°で投げ出せばよさそう。
それを式から導いてみます。
物体の運動を水平方向と鉛直方向に分解して考えるのがコツです。
水平方向には等速直線運動するので
\(x=v_0 \cos \theta \cdot t\)・・・①
鉛直方向には投げ上げ運動するので
\(0=v_0 \sin \theta – gt\)・・・②
②より
\(t=\dfrac{v_0 \sin \theta}{g}\)・・・③
①, ③より
\(x=v_0 \cos \theta \times \dfrac{v_0 \sin \theta}{g}\)
\(=\dfrac{v_0 ^2 \sin \theta \cos \theta}{g}\)
\(=\dfrac{v_0 ^2 \sin 2\theta}{2g}\)
\(\sin 2\theta =1\) のとき \(x\) は最大となるので
\(2\theta =90^ \circ\)
\(\theta =45^ \circ\)