本日の中2(数検準2級:高1)の数学は、関数の応用に入りました。
数検準2級の関数の応用は
・放物線と直線
・2次関数の最大値・最小値
・2次関数の決定
です。
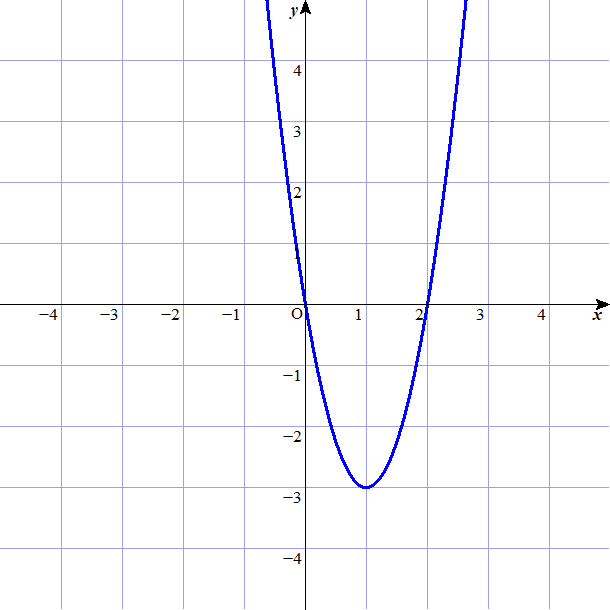
関数の問題では、まずはグラフを描いて考えることが大切です。
【例題】
頂点の座標が \((1, -3)\) で、点 \((-1, 9)\) を通る2次関数を求めなさい。
【解答】
頂点の座標が \((1, -3)\) なので
\(y=a(x-1)^2-3\) と表せる。
これが、点 \((-1, 9)\) を通るので
\(9=(-1-1)^2-3\)
\(a=3\)
よって
\(y=3(x-1)^2-3\)・・・(答)
頂点の座標が \((1, -3)\) なので
\(y=a(x-1)^2-3\) と表せる。
これが、点 \((-1, 9)\) を通るので
\(9=(-1-1)^2-3\)
\(a=3\)
よって
\(y=3(x-1)^2-3\)・・・(答)