本日、2025年最初の授業でした!
今日の中1生の数学は数検準2級(高1)2次関数の応用。
2次関数 \(y=ax^2+bx+c\) のグラフと \(x\) 軸との位置関係は、2次方程式 \(ax^2+bx+c=0\) の判別式 \(D=b^2-4ac\) の符号によって下記のように決まります。
\(D>0\) ⇔ 異なる2点で交わる
\(D=0\) ⇔ 接する
\(D<0\) ⇔ 共有点を持たない
例えば、\(y=3x^2+7x+5\) のグラフと \(x\) 軸の共有点の個数を求めると
判別式 \(D=7^2-4\times 3 \times 5=49-60=-11<0\)
したがって、共有点は持たない。
となります。
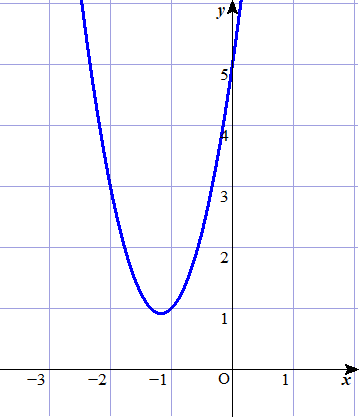
実際に、\(y=3x^2+7x+5\) のグラフを描くと次のようになり、\(x\) 軸と共有点を持たないことが確認できます。